Getline Function

#include <iostream>
#include<string>
using namespace std;

int main()
{
   string s;
   getline(cin,s);
   cout<<s;
}

String Character Shift

• Given a string $S$ of length $N$, shift each character of the string by $K$ positions to the right, where $K\le N$.

For example: Say $S$ = "hacker" and $K=2$. Here $N=6$.
Shifting each character in $S$ by $2$ positions to the right would result into $erhack$.
Note that $S\left[0\right]$ i.e. 'h' is moved by 2 positions to the $S\left[2\right]$. Also, $S\left[5\right]$ i.e. 'r', which is the last character in $S$ comes round-about back to $S\left[1\right]$ as there is no space for 'r' to go beyond the limits of string length.

Approach:

• Declare another auxillary string $shiftedS$ that is of the same size as $S$.
• Copy $i^{th}$ element of $S$ to the $(K+i{)}^{th}$ position in $shiftedS$. This means, $shiftedS[i+K]=S\left[i\right]$ where $0\le i<N$.
• Make sure that $i+K$ never exceeds $N$, because that will try to access a memory location which is not declared in $shiftedS$. There's a simple trick to ensure that - use $(i+K)modN$ .

#include <iostream>

#include<string>

using namespace std;

int main()

{

    string s,p;

    cin>>s;

    int k;

    cin>>k;

    for(int i=0;i<s.size();i++)

    {

        int index=(i+k)%s.size();

        p[index]=s[i];

        

    }

  for(int i=0;i<s.size();i++) { cout<<p[i];}

    

Common divisor

#include <iostream>

using namespace std;

int main()

{

   int a,b,c[50],d[50],count=0;

   cin>>a>>b;

   for(int i=0;i<50;i++){

       if(a%(i+1)==0){

           c[i]=i+1;

       }

       

   }

    for(int i=0;i<50;i++){

       if(b%(i+1)==0){

           d[i]=i+1;

       }

       

   }

   for(int i=0;i<50;i++){

       if(c[i]==d[i]){

           cout<<c[i]<<endl;

       

   }}

  

}

Palindrome

#include<iostream>
#include<string>
using namespace std;
int main(){
string s;
cin>>s;
int b=0;
for(int i=0;i<s.size();i++){if(s[i]!=s[s.size()-i-1])

{b=1;
break;}
}
if(b==0){
    cout<<"yes";
}
else cout<<"N0";
    }
    

Graph Theory

Graph Theory

Adjacency matrix

An adjacency matrix is a VxV binary matrix A. Element $A_{i,j}$ is 1 if there is an edge from vertex i to vertex j else $A_{i,j}$ is 0.

Note: A binary matrix is a matrix in which the cells can have only one of two possible values - either a 0 or 1.

The adjacency matrix can also be modified for the weighted graph in which instead of storing 0 or 1 in $A_{i,j}$, the weight or cost of the edge will be stored.

In an undirected graph, if $A_{i,j}$ = 1, then $A_{j,i}$ = 1. In a directed graph, if $A_{i,j}$ = 1, then $A_{j,i}$ may or may not be 1.

Adjacency matrix provides constant time access (O(1) ) to determine if there is an edge between two nodes. Space complexity of the adjacency matrix is O($V^2$).

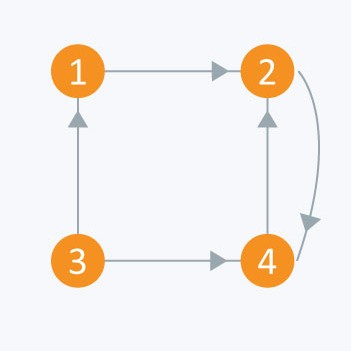
The adjacency matrix of the following graph is:

i/j: 1 2 3 4
1 : 0 1 0 0
2 : 0 0 0 1
3 : 1 0 0 1
4 : 0 1 0 0

code for adjacency matrix

#include<iostream>
using namespace std;
int main(){

    int x,y,node,edge;

    cin>>node>>edge;

    int a[10][10]={0};

    for(int i=0;i<edge;i++){

        cin>>x>>y;

        a[x][y]=1;
        
    }
  
}

TEST YOUR UNDERSTANDING

Edge Existence

You have been given an undirected graph consisting of $N$ nodes and $M$ edges. This graph can consist of self-loops as well as multiple edges. In addition , you have also been given $Q$ queries. For each query , you shall be given 2 integers $A$ and $B$. You just need to find if there exists an edge between node $A$ and node $B$. If yes, print "YES" (without quotes) else , print "NO"(without quotes).
Input Format:
The first line consist of 2 integers $N$ and $M$ denoting the number of nodes and edges respectively. Each of the next $M$ lines consist of 2 integers $A$ and $B$ denoting an undirected edge between node $A$ and $B$. The next line contains a single integer $Q$ denoting the number of queries. The next Line contains 2 integers $A$ and $B$ denoting the details of the query.
Output Format
Print Q lines, the answer to each query on a new line.
Constraints:
$1\le N\le {10}^3$
$1\le M\le {10}^3$
$1\le A,B\le N$
$1\le Q\le {10}^3$

#include<iostream>
using namespace std;
int main(){

    int x,y,node,edge;

    cin>>node>>edge;

    int a[10][10]={0};

    for(int i=0;i<edge;i++){

        cin>>x>>y;

        a[x][y]=1;
        
    }
  int r,p,q;
  cin>>r;
  for(int i=0;i<r;i++){
      cin>>p>>q;
      if(a[p][q]==1){
          cout<<"YES"<<endl;
          
      }
      else cout<<"NO"<<endl;
      
  }

}