Graph Theory

Graph Theory

Adjacency matrix

An adjacency matrix is a VxV binary matrix A. Element $A_{i,j}$ is 1 if there is an edge from vertex i to vertex j else $A_{i,j}$ is 0.

Note: A binary matrix is a matrix in which the cells can have only one of two possible values - either a 0 or 1.

The adjacency matrix can also be modified for the weighted graph in which instead of storing 0 or 1 in $A_{i,j}$, the weight or cost of the edge will be stored.

In an undirected graph, if $A_{i,j}$ = 1, then $A_{j,i}$ = 1. In a directed graph, if $A_{i,j}$ = 1, then $A_{j,i}$ may or may not be 1.

Adjacency matrix provides constant time access (O(1) ) to determine if there is an edge between two nodes. Space complexity of the adjacency matrix is O($V^2$).

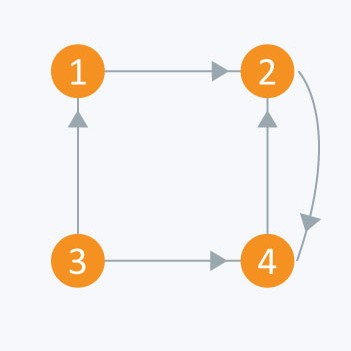
The adjacency matrix of the following graph is:

i/j: 1 2 3 4
1 : 0 1 0 0
2 : 0 0 0 1
3 : 1 0 0 1
4 : 0 1 0 0

code for adjacency matrix

#include<iostream>
using namespace std;
int main(){

    int x,y,node,edge;

    cin>>node>>edge;

    int a[10][10]={0};

    for(int i=0;i<edge;i++){

        cin>>x>>y;

        a[x][y]=1;
        
    }
  
}

TEST YOUR UNDERSTANDING

Edge Existence

You have been given an undirected graph consisting of $N$ nodes and $M$ edges. This graph can consist of self-loops as well as multiple edges. In addition , you have also been given $Q$ queries. For each query , you shall be given 2 integers $A$ and $B$. You just need to find if there exists an edge between node $A$ and node $B$. If yes, print "YES" (without quotes) else , print "NO"(without quotes).
Input Format:
The first line consist of 2 integers $N$ and $M$ denoting the number of nodes and edges respectively. Each of the next $M$ lines consist of 2 integers $A$ and $B$ denoting an undirected edge between node $A$ and $B$. The next line contains a single integer $Q$ denoting the number of queries. The next Line contains 2 integers $A$ and $B$ denoting the details of the query.
Output Format
Print Q lines, the answer to each query on a new line.
Constraints:
$1\le N\le {10}^3$
$1\le M\le {10}^3$
$1\le A,B\le N$
$1\le Q\le {10}^3$

#include<iostream>
using namespace std;
int main(){

    int x,y,node,edge;

    cin>>node>>edge;

    int a[10][10]={0};

    for(int i=0;i<edge;i++){

        cin>>x>>y;

        a[x][y]=1;
        
    }
  int r,p,q;
  cin>>r;
  for(int i=0;i<r;i++){
      cin>>p>>q;
      if(a[p][q]==1){
          cout<<"YES"<<endl;
          
      }
      else cout<<"NO"<<endl;
      
  }

}